Heat equation: Heating a rod

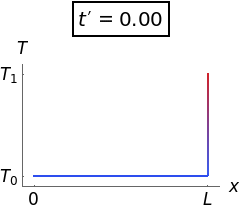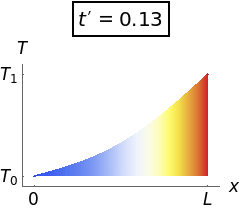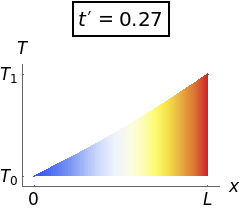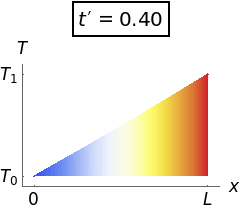
Your work doesn't need to be as detailed as this.

Source code for the images: code.wl
Return to the home page.

Problem

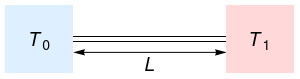
Consider a uniform rod of length L and thermal diffusivity \kappa.

Suppose the rod is initially at temperature T_0 throughout. At time t = 0:

What happens?

Diagram for heating a rod example

Quantities

Independent variables
x position (0 \le x \le L)
t time (t \ge 0)
Dependent variable
T temperature
Constants
L length
\kappa thermal diffusivity
T_0 lower temperature
T_1 higher temperature

Defining equations

Partial differential equation (PDE)

Heat equation in T = T (x, t), throughout the rod, for all time:

\frac{\pd T}{\pd t} = \kappa \frac{\pd^2 T}{{\pd x}^2}

Before we do anything, we should understand what this means:

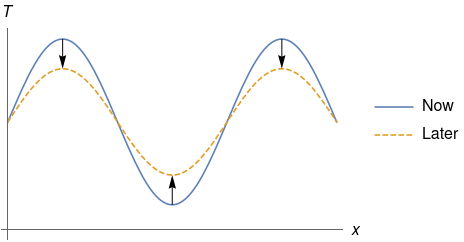
Basically, the heat equation says that as time passes, bumps in the temperature profile are levelled out.

Diagram showing temperature profile levelling out with time

Boundary conditions (BCs)

Fixed temperature at the two ends, for all time:

\begin{aligned} \eval{T}_{x = 0} &= T_0 \\ \eval{T}_{x = L} &= T_1 \end{aligned}

Initial condition (IC)

Temperature is T_0 throughout the rod, initially:

\eval{T}_{t = 0} = T_0

Scaling

\gdef \unscaled #1 {\colg{#1}} \gdef \scaled #1 {\colv{#1'}}

Units like metres and feet or Celsius and Fahrenheit are arbitrary, and it is better to work in the natural units which arise from the physical constants provided in the problem.

We move from dimensional (unscaled) variables to dimensionless (scaled) variables (marked with a prime):

Temperature

The natural temperature scale in the problem is T_1 - T_0, the difference between the two prescribed temperatures. Define scaled temperature \scaled{T} by

\unscaled{T} = T_0 + (T_1 - T_0) \scaled{T},

so that in scaled terms, the lower temperature is \scaled{T} = 0 and the higher temperature is \scaled{T} = 1.

Position

The natural length scale in the problem is L, the length of the rod. Define scaled position \scaled{x} by

\unscaled{x} = L \scaled{x},

so that in scaled terms, the left end of the rod is \scaled{x} = 0 and the right end of the rod is \scaled{x} = 1.

Time

The time scale isn't immediately obvious, so define scaled time \scaled{t} by

\unscaled{t} = \tau \scaled{t},

with the time scale \tau yet to be determined, i.e. free.

Dimensionless groups

\gdef \group #1 {\colr{\squarebr{#1}}}

We take the heat equation

\frac{\pd\unscaled{T}}{\pd\unscaled{t}} = \kappa \frac{\pd^2 \unscaled{T}}{{\pd\unscaled{x}}^2}

and move from unscaled to scaled variables (use the chain rule):

\frac{(T_1 - T_0)}{\tau} \frac{\pd\scaled{T}}{\pd\scaled{t}} = \kappa \frac{(T_1 - T_0)}{L^2} \frac{\pd^2 \scaled{T}}{{\pd\scaled{x}}^2}

Rearrange:

\group{\frac{L^2}{\kappa \tau}} \frac{\pd\scaled{T}}{\pd\scaled{t}} = \frac{\pd^2 \scaled{T}}{{\pd\scaled{x}}^2}

All of the scaled variables are dimensionless, therefore the bracketed term is a dimensionsless group, i.e. just a number.

Time scale

Currently the time scale \tau is free; it is not prescribed in the problem and we haven't defined it yet. Because we have one free scale \tau and one dimensionless group, we can eliminate the dimensionless group* by setting it equal to one and solving for \tau:

\group{\frac{L^2}{\kappa \tau}} = 1
\tau = \frac{L^2}{\kappa}

(*NOTE: if a problem has fewer free scales than dimensionless groups, you won't be able to eliminate all of the dimensionless groups.)

Making sense

At this point we pause to check: does the time scale we have found make sense?

Yes this makes sense.

Finish scaling

Having eliminated the dimensionless group, our heat equation is now

\frac{\pd\scaled{T}}{\pd\scaled{t}} = \frac{\pd^2 \scaled{T}}{{\pd\scaled{x}}^2}.

We should also scale the boundary conditions and initial condition:

\begin{aligned} \eval{\scaled{T}}_{\scaled{x} = 0} &= 0 \\ \eval{\scaled{T}}_{\scaled{x} = 1} &= 1 \\ \eval{\scaled{T}}_{\scaled{t} = 0} &= 0 \end{aligned}

Writing primes everywhere is annoying, so from here onward we drop the primes. Altogether:

\begin{gathered} \frac{\pd T}{\pd t} = \frac{\pd^2 T}{{\pd x}^2} \\[\tallspace] \eval{T}_{x = 0} = 0 \\ \eval{T}_{x = 1} = 1 \\ \eval{T}_{t = 0} = 0 \end{gathered}

Equilibrium solution

\gdef \trans #1 {\colr{#1}} \gdef \equil #1 {\colb{#1}} \gdef \Ttr {\trans{T_\mathrm{tr}}} \gdef \Teq {\equil{T_\mathrm{eq}}}

After a long time, the heat going in at the right end x = 1 will be in balance with the heat lost at the left end x = 0. The temperature profile T will reach an equilibium profile \Teq, which may depend on the position x but not on the time t. In symbols,

\lim_{t \to \infty} T (x, t) = \Teq (x).

Thus the PDE and boundary conditions simplify to

\begin{gathered} 0 = \frac{\td^2 \Teq}{{\td x}^2} \\[\tallspace] \eval{\Teq}_{x = 0} = 0 \\ \eval{\Teq}_{x = 1} = 1. \end{gathered}

(The initial condition (t = 0) is irrelevant at equilibrium.)

The three equations above say that \Teq (x) is a straight line function of x passing throught (x, \Teq) = (0, 0) and (x, \Teq) = (1, 1), so by inspection the equilibrium temperature profile is

\Teq (x) = x.

Transient solution

Subtract out equilibrium solution

Since the equilibrium solution isn't zero, this means that the PDE and boundary conditions aren't all homogeneous (in our case the boundary condition at x = 1 isn't homogeneous). Before doing separation of variables, make sure to subtract out the equilibrium solution so that the boundary conditions become homogeneous. To do this, write the solution as a sum of equilibrium and transient parts,

T (x, t) = \Teq (x) + \Ttr (x, t)

or

T = \Teq + \Ttr.

Substituting these into the scaled equations, we get

\begin{gathered} \cancel{\frac{\pd \Teq}{\pd t}} + \frac{\pd \Ttr}{\pd t} = \cancel{\frac{\pd^2 \Teq}{{\pd x}^2}} + \frac{\pd^2 \Ttr}{{\pd x}^2} \\[\tallspace] \cancel{\eval{\Teq}_{x = 0}} + \eval{\Ttr}_{x = 0} = \cancel{0} \\ \cancel{\eval{\Teq}_{x = 1}} + \eval{\Ttr}_{x = 1} = \cancel{1} \\ \eval{\Teq}_{t = 0} + \eval{\Ttr}_{t = 0} = 0. \end{gathered}

Since \eval{\Teq}_{t = 0} = \eval{x}_{t = 0} = x, these become

\begin{gathered} \frac{\pd \Ttr}{\pd t} = \frac{\pd^2 \Ttr}{{\pd x}^2} \\[\tallspace] \eval{\Ttr}_{x = 0} = 0 \\ \eval{\Ttr}_{x = 1} = 0 \\ \eval{\Ttr}_{t = 0} = -x. \end{gathered}

Separation of variables

\gdef \pos #1 {\colg{#1}} \gdef \time #1 {\colv{#1}} \gdef \con #1 {\colb{#1}}

Suppose that the transient solution is the product of a function of position only and a function of time only,

\Ttr (x, t) = \pos{X (x)} \time{Y (t)}.

(This may seem restrictive, but since the heat equation is linear we can take linear combinations afterwards.) Substituting this into the PDE for \Ttr, we get

\begin{aligned} \frac{\pd (\pos{X} \time{Y})}{\pd \time{t}} &= \frac{\pd^2 (\pos{X} \time{Y})}{{\pd \pos{x}}^2} \\[\tallspace] \pos{X} \time{\frac{\td Y}{\td t}} &= \pos{\frac{\td^2 X}{{\td x}^2}} \time{Y}. \end{aligned}

Dividing through by \pos{X} \time{Y}:

\time{\frac{1}{Y} \frac{\td Y}{\td t}} = \pos{\frac{1}{X} \frac{\td^2 X}{{\td x}^2}}

This says that a function of t only is equal to a function of x only, and this is supposed to be true for all \time{t} and all \pos{x}.

Q. How can a function of t be equal to a function of x for all \time{t} and all \pos{x}?
A. Both must equal the same constant:
\time{\frac{1}{Y} \frac{\td Y}{\td t}} = \pos{\frac{1}{X} \frac{\td^2 X}{{\td x}^2}} = \con{-\lambda^2}.
Q. Why can't the constant be positive?
A. Because a positive constant doesn't yield useful solutions. In other units at UWA you're probably expected to show this every time, but here at MATH3022 we don't like wasting your time. Just put -\lambda^2 for the ODE which has the homogeneous boundary conditions. This ensures oscillatory solutions in that direction.

Thus we have separated the PDE into two ODEs:

Time

\begin{aligned} \time{\frac{\td Y}{\td t}} &= \con{-\lambda^2} \time{Y} \\[\tallspace] \time{Y (t)} &= C \ee ^ {\con{-\lambda^2} t} \end{aligned}

Position

\begin{aligned} \pos{\frac{\td^2 X}{{\td x}^2}} &= \con{-\lambda^2} \pos{X} \\[\tallspace] \pos{X (x)} &= A \cos (\con{\lambda} x) + B \sin (\con{\lambda} x) \end{aligned}

Altogether

\Ttr (x, t) = \ee ^ {\con{-\lambda^2} t} \squarebr{A \cos (\con{\lambda} x) + B \sin (\con{\lambda} x)}

(Here the constant C has been absorbed into A and B.)

Boundary conditions

We then apply the boundary conditions at the two ends of the rod:

Left end

We have

\eval{\Ttr}_{x = 0} = \ee ^ {\con{-\lambda^2} t} \cdot A = 0

which implies A = 0. Therefore

\Ttr (x, t) = B \ee ^ {\con{-\lambda^2} t} \sin (\con{\lambda} x).

Right end

We have

\eval{\Ttr}_{x = 1} = B \ee ^ {\con{-\lambda^2} t} \sin \con{\lambda} = 0

and since we don't want B = 0 (which is boring), we must have

\sin \con{\lambda} = 0
\con{\lambda} = \con{n} \pi, \quad n = 1, 2, 3, \dots.

Physical sense

To recap, our transient solution is the product of an exponential decay in time and a sinusoid in position, linked through the constant \con{\lambda} = \con{n} \pi:

\Ttr (x, t) = B \ee ^ {\con{-n^2} \pi^2 t} \sin (\con{n} \pi x)

What does this mean physically?

Initial condition

So far our transient solution \Ttr satisfies the PDE and boundary conditions. But what about the initial condition,

\eval{\Ttr}_{t = 0} = -x?

Clearly the single product \Ttr (x, t) = B \ee ^ {\con{-n^2} \pi^2 t} \sin (\con{n} \pi x) isn't going to work. We need something a bit more general:

Fourier series

\gdef \B #1 {B_{\con{#1}}} \gdef \sine #1 {\sin (\con{#1} \pi x)}

Recall that:

  1. The heat equation is linear
  2. The boundary conditions for \Ttr at x = 0 and x = 1 are homogeneous because we subtracted out the equilibrium solution

Therefore, linear combinations of the product \Ttr (x, t) = B \ee ^ {\con{-n^2} \pi^2 t} \sine{n} will also satisfy the heat equation and the boundary conditions. Writing \B{n} instead of B, a more general form for \Ttr is

\Ttr (x, t) = \sum_{\con{n} = 1}^{\infty} \B{n} \ee ^ {\con{-n^2} \pi^2 t} \sine{n}.

The initial condition becomes

\eval{\Ttr}_{t = 0} = \sum_{\con{n} = 1}^{\infty} \B{n} \sine{n} = -x,

and we need to find a Fourier series for the function -x, i.e. determine the coefficients \B{1}, \B{2}, \dots.

Inner product spaces

\gdef \innerp #1 #2 {\delimwrap{\langle}{#1,#2}{\rangle}} \gdef \vece #1 {\vec{e}_{\con{#1}}}

It turns out that finding a Fourier series is very similar to the problem of writing a vector \vec{v} in terms of the orthogonal basis \curlybr{\vece{1}, \vece{2}, \dots}:

\begin{aligned} \vec{v} &= \B{1} \vece{1} + \B{2} \vece{2} + \dots \\ -x &= \B{1} \sine{1} + \B{2} \sine{2} + \dots \end{aligned}

In the case of the Fourier series, the "vector space" is called an inner product space, the "vector" is the function -x, and the "orthogonal basis" is the sequence of functions \curlybr{\sine{1}, \sine{2}, \dots}. In both cases we want to determine the coefficients \B{1}, \B{2}, \dots.

In the familiar vector space, the dot product of two vectors f and g is given by

\vec{f} \dotp \vec{g} = f_1 g_1 + f_2 g_2 + \dots.

In an inner product space, the analogue to the dot product is the inner product. In the current problem*, the inner product of two functions f (x) and g (x) is given by

\innerp{f}{g} = \int_0^1 f (x) g (x) \td x.

(*NOTE: More generally you need to include a weighting function inside the integral; only here the weighting function happens to be 1. The endpoints of the integral come from the endpoints of the two boundary conditions.)

The dot/inner product is useful because of the orthogonality property; the dot/inner product between two basis vectors is non-zero if and only if they are the same basis vector:

\begin{gathered} \vece{m} \dotp \vece{n} = \begin{cases} \norm{\vece{m}} ^ 2, & \con{m} = \con{n} \\ 0, & \con{m} \ne \con{n} \end{cases} \\[\tallspace] \int_0^1 \sine{m} \sine{n} \td x = \begin{cases} 1/2, & \con{m} = \con{n} \\ 0, & \con{m} \ne \con{n} \end{cases} \end{gathered}

To find the coefficient for a particular basis vector, simply take the dot/inner product of the series with that vector to kill off all the other components. For example, to find \B{2}, take the dot product with \vece{2}:

\begin{aligned} \vec{v} &= \B{1} \vece{1} + \B{2} \vece{2} + \dots \\ \vec{v} \dotp \vece{2} &= \cancel{\B{1} \vece{1} \dotp \vece{2}} + \B{2} \vece{2} \dotp \vece{2} + \cancel{\dots} \\[\tallspace] \B{2} &= \frac{\vec{v} \dotp \vece{2}}{\norm{\vece{2}} ^ 2} \end{aligned}

Translating this to the context of Fourier series:

\begin{aligned} -x &= \B{1} \sine{1} \\ & \quad + \B{2} \sine{2} \\ & \quad + \dots \\ \int_0^1 -x \sine{2} \td x &= \cancel{\B{1} \int_0^1 \sine{1} \sine{2} \td x} \\ & \quad + \B{2} \int_0^1 \sine{2} \sine{2} \td x \\ & \quad + \cancel{\dots} \\[\tallspace] \B{2} &= \frac{\int_0^1 -x \sine{2} \td x}{\int_0^1 \sin^2 (\con{2} \pi x) \td x}. \end{aligned}

In general, the \con{n}th coefficient is given by

\B{n} = \frac{\int_0^1 -x \sine{n} \td x}{\int_0^1 \sin^2 (\con{n} \pi x) \td x}

We're not in first year anymore, so get Mathematica to do this for us: 

FullSimplify[
  Divide[
    Integrate[-x Sin[n Pi x], {x, 0, 1}],
    Integrate[Sin[n Pi x] ^ 2, {x, 0, 1}]
  ]
  , Element[n, Integers]
]

Thus

\B{n} = \frac{2 (-1) ^ {\con{n}}}{\con{n} \pi}.

Result

Putting everything together, the solution is

\begin{aligned} T &= \Teq + \Ttr \\ &= \equil{x} + \trans{ \sum_{n = 1}^{\infty} \frac{2 (-1) ^ n}{n \pi} \ee ^ {-n^2 \pi^2 t} \sin (n \pi x) }. \end{aligned}

Remarks on convergence

  1. This is an exact result, but it is an infinite series.
    Whether an infinite series is useful depends on how fast it converges (and how many terms you need for a given accuracy).
  2. For t = 0, this series takes ages to converge.
    This is because there is no exponential decay when t = 0, and we have an alternating series with coefficients going like 1 / n. Sure, it converges, but it is much too slow to be practical.
  3. For moderate to large t, convergence is very fast.
    This is because \ee ^ {-n^2 \pi^2 t} decays exponentially quickly. Only a few terms are needed (or even just one term).

How long to reach equilibrium?

While "infinity" is technically correct, it isn't a useful answer. For example, infinity is technically the time it takes for nuclear radiation to clear out at Maralinga, but a much more practical measure is the half-life of 24100 years for plutonium-239.

If you should learn anything from this page, it's that you should never answer "how long till equilibrium" with "infinity". Don't do it. (Also don't bother including a smart remark like "technically the answer is infinity"; we know already.)

The rule of thumb we use in applied maths is that we're practically at equilibrium when the exponent reaches 4 (or 5, depending on who you ask), \ee ^ {-4} being just under 2\%. Now, when t > 0, our series is dominated by the first term n = 1 (the terms with higher n are much much smaller). Therefore, a practical measure of equilibrium time is obtained by setting the exponent to 4 for n = 1:

\begin{aligned} 1^2 \pi^2 t &\sim 4 \\ t &\sim \frac{4}{\pi^2} \end{aligned}

Finally, don't forget that we are still working in scaled (dimensionless) variables; the t above is what we once called \scaled{t}, equal to \unscaled{t} / \tau. The unscaled (dimensional) equilibrium time is therefore

\unscaled{t} \sim \frac{4 \tau}{\pi^2} = \frac{4 L^2}{\pi^2 \kappa}.

Visualising the solution

In summary, the rod is initially at temperature T_0 throughout, but has its right end raised to and held at a higher temperature T_1. The left end is held at the original temperature T_0. As time passes, the temperature profile rises towards a straight-line profile at equilibrium.

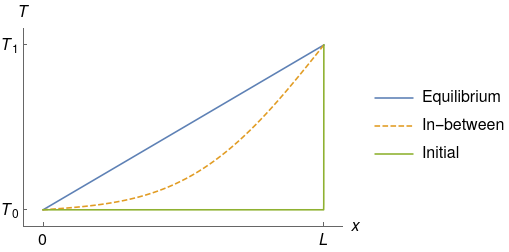
Plot of initial, in-between, and equilibrium temperature profile

In animated form (deliberately made small to save bandwidth):

Animation of temperature profile

END

Return to the home page.