Traffic: light change

Source code for images: code.wl
Return to traffic model summary

Problem

\gdef \Vmax {V_\mathrm{max}} \gdef \Nmax {N_\mathrm{max}} \gdef \Fmax {F_\mathrm{max}}

Cars queued bumper-to-bumper wait at a red traffic light which turns green at t = 0. In symbols,

\eval{N}_{t = 0} = \begin{cases} \Nmax, & x < 0 \\ 0, & x > 0 \end{cases}.

What happens?

Animation

Animation for traffic light change

Characteristics in purple
Dense/slow regions in red
Sparse/fast regions in blue
Trajectories in yellow

Characteristics

Dense region

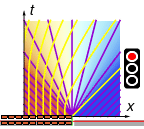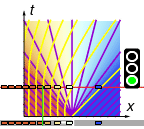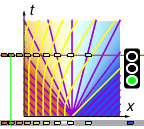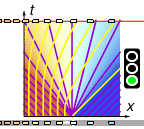
First consider t = 0, x < 0, i.e. the left half of the x-axis, where the cars are initially waiting at maximum density. Here we have

\begin{aligned} N &= \Nmax \\ V &= 0 \\ \frac{\td F}{\td N} &= -\Vmax. \end{aligned}

Thus the characteristics are straight lines with slope -\Vmax, and so the left half of the x-axis extends into a lower-left triangular region ◣ with maximum density and zero speed:

N (x, t) = \begin{cases} \Nmax, & x < -\Vmax t \end{cases}

Empty region

Next consider t = 0, x > 0, i.e. the right half of the x-axis, which is initially empty. Here we have

\begin{aligned} N &= 0 \\ V &= \Vmax \\ \frac{\td F}{\td N} &= +\Vmax. \end{aligned}

Thus the characteristics are straight lines with slope +\Vmax, and so the right half of the x-axis extends into a lower-right triangular region ◢ with zero density and full speed:

N (x, t) = \begin{cases} 0, & x > +\Vmax t \end{cases}

Transition fan

\gdef \charac #1 {\colv{#1}} \gdef \xc {x_\mathrm{c}}

What about the remaining triangular region ▽ in the middle?

Well, we haven't yet looked at the origin t = 0, x = 0. There we have an instantaneous jump from maximum density to zero density, so we have

\begin{alignedat}{1} \Nmax &\ge N \ge 0 \\ 0 &\le V \le \Vmax \\ -\Vmax &\le \frac{\td F}{\td N} \le +\Vmax. \end{alignedat}

Thus we get a fan of characteristics emanating from the origin, with slopes running through all values from -\Vmax up to +\Vmax. In particular, the characteristic for a given density N is given by

\charac{ \xc (t) = \frac{\td F}{\td N} \cdot t = \Vmax \roundbr{1 - \frac{2 N}{\Nmax}} t }.

Therefore for the central triangular region ▽ we have

N (x, t) = \begin{cases} \dfrac{\Nmax}{2} \roundbr{1 - \dfrac{x}{\Vmax t}}, & -\Vmax t < x < +\Vmax t \end{cases}.

Result

Altogether:

N (x, t) = \begin{cases} \Nmax, & x < -\Vmax t \\ \frac{\Nmax}{2} \roundbr{1 - \frac{x}{\Vmax t}}, & -\Vmax t < x < +\Vmax t \\ 0, & x > +\Vmax t \end{cases}

Remarks

Animation for traffic light change (again)

Characteristics in purple
Dense/slow regions in red
Sparse/fast regions in blue
Trajectories in yellow

The main results are:

The 'signal to go' propagates backwards at the speed limit, along the characteristic \xc (t) = -\Vmax t.
Does this happen in real life?
Yes, the further back you are in the queue, the longer you need to wait before you can go.
All cars pass the stop line at half the speed limit, corresponding to the characteristic \xc (t) = 0 for N = \Nmax / 2, V = \Vmax / 2.
Does this happen in real life?
Well, roughly. In the model, the first car is able to accelerate instantly from zero to the speed limit; this isn't possible in real life. If you're not first-in-line though, the model is pretty fair; in my experience I am usually in second gear by the time I pass the stop line for a traffic light in a 60kph zone.

END

Return to traffic model summary

Return to the home page.